

Any input gain imbalance in the 2 quadrature components for a complex sinusoidal signal will contain some of that same conjugate interference as well. Strictly real valued sinusoids very near DC (or Fs/2) will also see interference from their own conjugate images in the spectrum. My guess is that, if the S/N ratio is low enough, a parametric estimator will produce a more accurate estimation, given that you have more samples than unknowns (3 sinusoidal parameters + 1 DC offset parameter).Īnother possibility is to try to remove the DC offset by averaging or low pass filtering over a much longer window of samples, perhaps several hundred to thousands. For frequencies around or lower than FFT result bin +-2, any significant DC offset will constitute that strong nearby interference (in bin 0) preventing resolving either frequency as an independent peak. Normally one needs at least 2 FFT result bins of separation to just start to resolve 2 frequency peaks. So again: What is required to make the error on the estimates more like 0.01 Hz?įFTs don't work well for sinusoidal frequency estimation if there is a nearby strong interfering signal. I am sure there are ways of saving power by only calculating the 6 bins we are interested in, but that optimization only makes sense if we can get the required accuracy from the algorithm in the first place.

By changing the frequency it's clear that the error near zero only for near integer frequencies.Ī caveat is that the input signal also has a varying DC offset, so ideally the DC offset should be "filtered" as well. The console output showing the power from the 6 bins as well as the final estimated frequency and error is here: i = 33 f = 0.000000 p = 44.717018Įstimated = 0.24 Hz Actual = 0.45 Hz Error = 0.21 HzĪs can be seen the error is way bigger than desired for this specific test frequency of 0.45 Hz. The output from the FFT (shifted) looks like this: Printf("Estimated = %.2f Hz Actual = %.2f Hz Error = %.2f Hz\n", fmax, f_signal, abs(fmax-f_signal)) Interpolate to find better estimate of peak frequency Create the associated frequency vector f(1) = frequency of bin 1 Perform FFT (and shift bins around to have -32Hz to +31Hz)
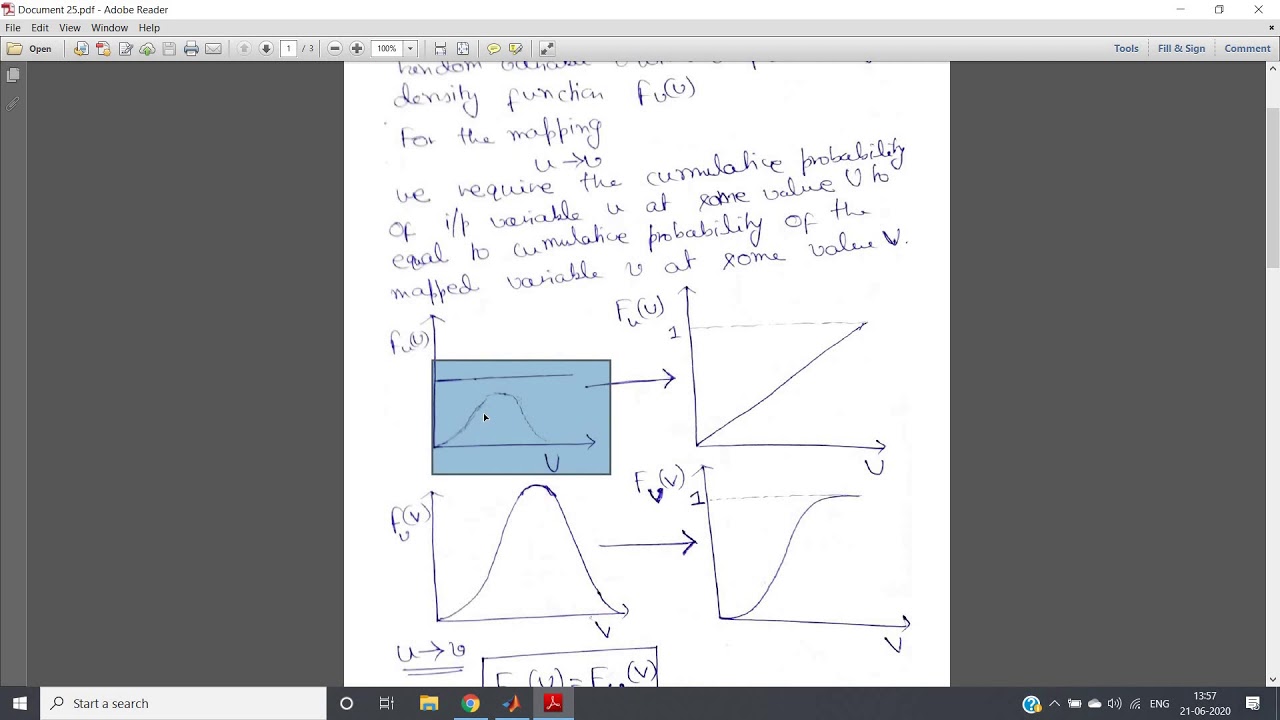
The algorithm looks like this in Scilab: sample_rate = 64 į_signal = 0.45 // Hz - The signals peak frequency The algorithm must run on a low power CPU, so computational power is quite limited and power consumption is an important parameter. We look at the 6 bins representing 0Hz to 6Hz and want to interpolate here to find the peak. They will then represent frequencies from -32Hz to +31Hz. With one second, we have 64 complex samples go into the FFT and 64 complex magnitudes coming out. The idea is to use the FFT to both do the filtering of unwanted higher frequency noise and do the estimation of the 0.5-4Hz signal peak frequency. This is my first attempt to solve this problem with FFT, and the question is: What is required to make the frequency estimate accuracy around 0.01 Hz? I want an output showing the current peak frequency with a maximum lag of about 1 second. I have a noisy signal in I/Q format with a peak frequency that constantly changes between 0.5Hz and 4Hz. 103 EE22xx53 Microcontroller and Embedd ed System.
99 EE22xx5 1 Modern Optimiza tion Technique. 97 EE22xx5 0 Advance d Instr umentat ion. 94 EE22xx2 5 Advance d Electr ical Machine. 92 EE22xx24 Computer Relaying and Wide Area Protection. 90 EE22xx23 Digital Protection of Power System. 82 EE22xx17 Power system Planning and Reliability. 80 EE22xx1 6 Smart Grid Design and Analysis. 76 EE22xx14 Flexible AC Transmission Systems. 71 EE22xx11 Non-Conventional Energy S ystem. 70 EE220301 Dissertation (To be continued in 4th Semester). 50 EC21xx 61 Digita l Signal Proces sing. 48 EE21xx57 Photovoltaic Energy Technolog y and Management. 44 EE21xx55 Electric Vehicle and Energy Storage System. 42 EE21xx5 4 Industr ial Drive and Control. 40 EE21xx53 Microcontroller and Embedded System. 36 EE21xx5 1 Modern Optimiza tion Technique. 34 EE21xx21 Virtual Instrumentation Using Labview. 24 EE21xx15 Robotics, Control and Movements. 22 EE21xx14 Mathematics for System Theory. 20 EE21xx13 Process Modelling and Id entification. 16 EE210301 Dissertation (To be continued in 4th Semester).


 0 kommentar(er)
0 kommentar(er)
